填充和步幅
假设输入形状为n_hXn_w,卷积核形状为k_hXk_w,那么输出形状将是
(n_h-k_h+1) X (n_w-k_w+1)
因此,卷积的输出形状取决于输入形状和卷积核的形状。
填充
通常,如果我们添加p_h行填充(大约一半在顶部,一半在底部)和p_w列填充(左侧大约一半,右侧一半),则输出形状将为
(n_h-k_h+p_h+1) X (n_w-k_w+p_w+1)
这意味着输出的高度和宽度将分别增加p_h和p_w。
在许多情况下,我们需要设置p_h=k_h-1和p_w=k_w-1,使输入和输出具有相同的高度和宽度。
这样可以在构建网络时更容易地预测每个图层的输出形状。假设k_h是奇数,我们将在高度的两侧填充p_h/2行。
如果k_h是偶数,则一种可能性是在输入顶部填充p_h/2行,在底部填充p_h/2行。同理,我们填充宽度的两侧。
卷积神经网络中卷积核的高度和宽度通常为奇数,例如1、3、5或7。
选择奇数的好处是,保持空间维度的同时,我们可以在顶部和底部填充相同数量的行,在左侧和右侧填充相同数量的列。
此外,使用奇数的核大小和填充大小也提供了书写上的便利。对于任何二维张量X,当满足:
- 卷积核的大小是奇数;
- 所有边的填充行数和列数相同;
- 输出与输入具有相同高度和宽度
则可以得出:输出Y[i, j]是通过以输入X[i, j]为中心,与卷积核进行互相关计算得到的。
步幅
通常,当垂直步幅为s_h、水平步幅为s_w时,输出形状为
[(n_h-k_h+p_h+s_h)/s_h] X [(n_w-k_w+p_w+s_w)/s_w]
如果我们设置了p_h=k_h-1和p_w=k_w-1,则输出形状将简化为
[(n_h+s_h-1)/s_h] X [(n_w+s_w-1)/s_w]
更进一步,如果输入的高度和宽度可以被垂直和水平步幅整除,则输出形状将为
(n_h/s_h) X (n_w/s_w)
LeNet
LeNet是最早发布的卷积神经网络之一,因其在计算机视觉任务中的高效性能而受到广泛关注。 这个模型是由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的(并以其命名),目的是识别图像中的手写数字。
总体来看,(LeNet(LeNet-5)由两个部分组成:
卷积编码器:由两个卷积层组成;
全连接层密集块:由三个全连接层组成。
该架构如图所示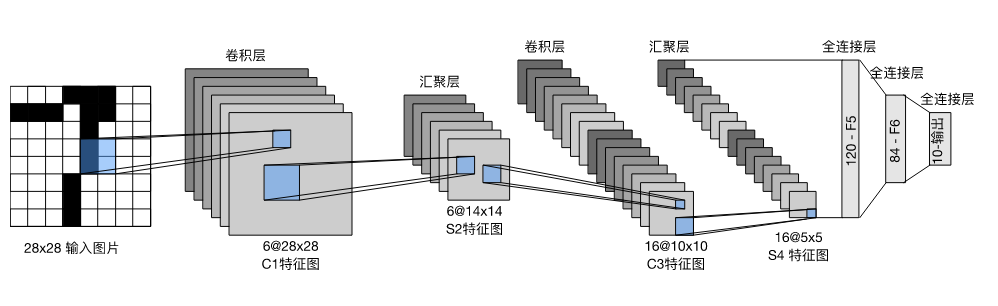
每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层。请注意,虽然ReLU和最大汇聚层更有效,但它们在20世纪90年代还没有出现。每个卷积层使用5×5卷积核和一个sigmoid激活函数。这些层将输入映射到多个二维特征输出,通常同时增加通道的数量。第一卷积层有6个输出通道,而第二个卷积层有16个输出通道。每个2×2池操作(步幅2)通过空间下采样将维数减少4倍。卷积的输出形状由批量大小、通道数、高度、宽度决定。
为了将卷积块的输出传递给稠密块,我们必须在小批量中展平每个样本。换言之,我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本,第二个维度给出每个样本的平面向量表示。LeNet的稠密块有三个全连接层,分别有120、84和10个输出。因为我们在执行分类任务,所以输出层的10维对应于最后输出结果的数量。
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))-------------完-------------
